


Aktiv Mathematics
Step-by-step interactive platform helping students master math from Prealgebra through Precalculus using active learning principles, scaffolded guidance, and real-time feedback
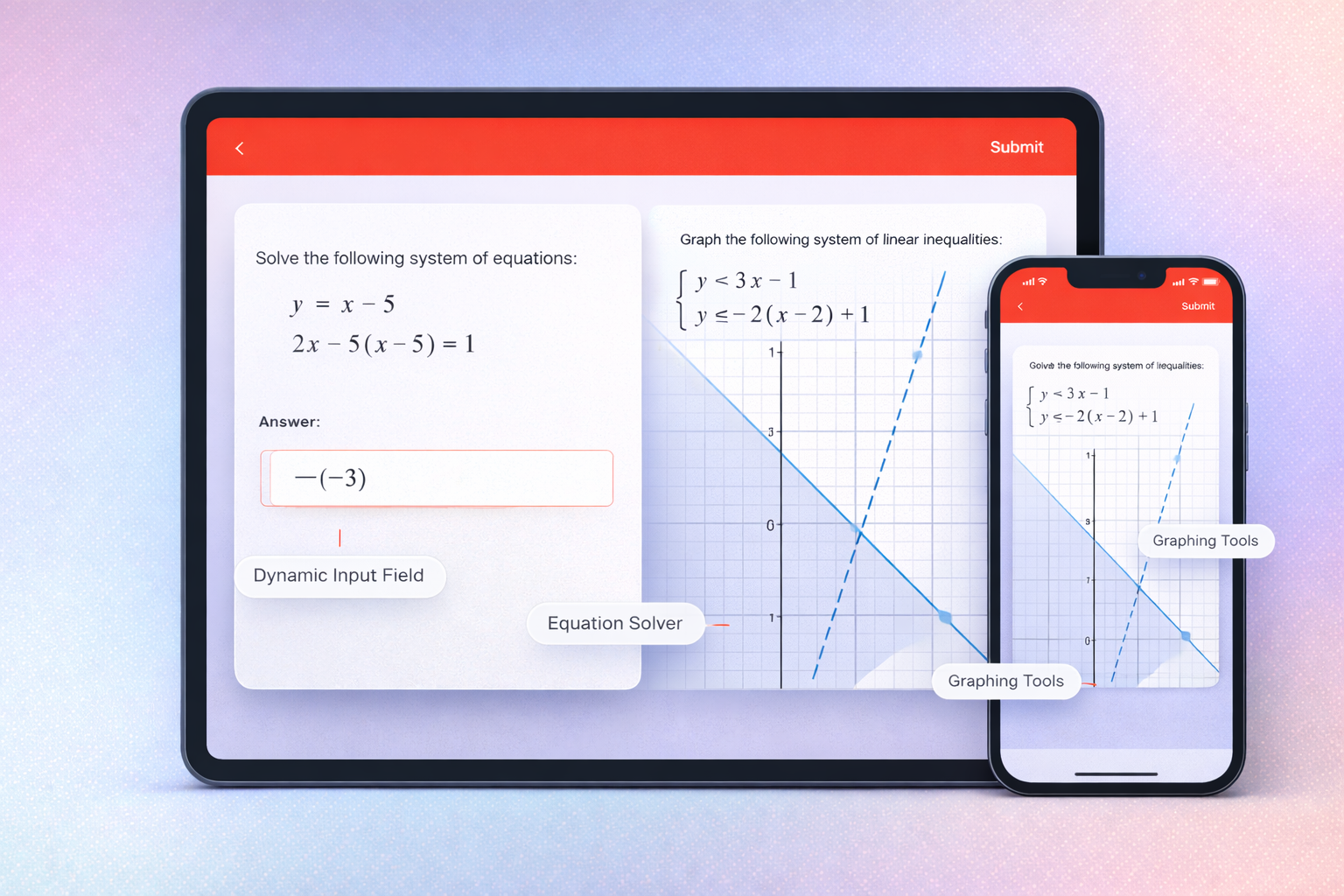
Overview
Digital math education had a fundamental problem: existing tools emphasized getting the right answer over building genuine mathematical understanding. At Aktiv Learning, I led the design of a platform that would change that.
Students often defaulted to paper because they didn't trust digital systems to help them actually think through math problems. These tools penalized mistakes rather than guiding students toward understanding. Instructors could only see final answers, making it nearly impossible to diagnose misconceptions or see where students' reasoning broke down.
We set out to build something better: a step-by-step interactive platform that respects how students naturally think—messy, iterative, and nonlinear—while providing the scaffolding and feedback they need to develop real mathematical understanding.
Three Learning Modes for Different Needs
The core insight behind Aktiv Mathematics is that students need different types of support depending on where they are in the learning process. I designed three distinct learning modes that work together to build understanding:
- Scaffolded Mode: Step-by-step guidance for foundational skills. Students work through problems with structured prompts and hints at each step, building confidence and establishing correct problem-solving patterns.
- StepWise Mode: Students demonstrate their reasoning process with targeted feedback after each step. This mode captures not just whether the answer is right, but how they got there, giving instructors visibility into student thinking.
- Final Answer Mode: Standard input for assessment and mastery checks. Once students have demonstrated understanding, they can work more independently with less scaffolding.
These modes allow instructors to match the level of support to each student's needs and gradually release responsibility as competence grows. It's differentiated instruction at scale, something nearly impossible with traditional homework systems.
Scaffolded, StepWise, and Final Answer modes providing progressive support
Math Input That Feels Natural
One of the biggest challenges in digital math education is input. How do you let students enter complex mathematical expressions without forcing them to learn LaTeX or fight with clunky equation editors?
I designed a simplified equation editor that supports fractions, radicals, exponents, and other mathematical notation with natural keyboard entry. Students can type expressions the way they think about them, and the editor intelligently formats them into proper mathematical notation.
Key design decisions included:
- Keyboard shortcuts that make sense: Forward slash creates fractions, caret for exponents, using patterns students already know from calculators and word processors
- Visual feedback: Real-time preview showing exactly how the expression will be evaluated, catching parentheses errors and order of operations mistakes before submission
- Forgiving input: The system accepts multiple equivalent formats and helps students correct minor syntax errors without penalizing them
- Mobile-friendly: Custom keyboard layouts on tablets and phones that surface mathematical symbols without requiring menu diving
For graphing problems, I integrated Desmos as the visualization engine, providing real-time interactive graphs that students could manipulate and explore. This turned static graphing exercises into dynamic learning experiences where students could immediately see the impact of changing variables.
Intuitive math input and real-time graphing powered by Desmos
Instructor Dashboards: Visibility Into Student Thinking
Traditional homework systems show instructors only final answers, making it difficult to diagnose where students struggle. I designed comprehensive instructor dashboards that provide visual representations of student reasoning and progress.
Key features of the instructor experience:
- Step-by-step work review: Instructors can see every step of a student's problem-solving process in StepWise mode, identifying exactly where misconceptions occur
- Class-wide analytics: Heat maps showing which problems students found most challenging, helping instructors adapt their teaching to address common struggles
- Individual progress tracking: Detailed views of each student's growth over time, completion rates, and areas where they excel or need additional support
- Inline feedback tools: Guidance bubbles that let instructors add contextual hints and corrections without penalizing errors, treating mistakes as learning opportunities
This transformed homework from a black box assessment tool into a window into student understanding. Instructors could have informed conversations with struggling students based on actual data about where their reasoning broke down.
Visual representation of student reasoning and class-wide progress
Research & Collaboration
Throughout the development of Aktiv Mathematics, I participated in extensive user research to ensure the platform met real pedagogical needs.
My research process included:
- Student interviews: Regular sessions with students from Prealgebra through Precalculus levels to understand their learning challenges, frustrations with existing tools, and how they naturally approach problem-solving
- Cognitive load studies: Observing where students experienced friction or confusion, identifying opportunities to reduce unnecessary complexity without sacrificing mathematical rigor
- Instructor workshops: Working closely with math professors and curriculum designers to understand pedagogical best practices, grading workflows, and how to surface actionable insights from student work
- Iterative testing: Rapid prototyping and testing cycles, getting feedback on interaction patterns before committing to full implementation
Close collaboration with subject matter experts—professors who understood both mathematics and pedagogy—ensured the platform respected how learning actually happens. Their input shaped everything from the progressive hint system to the choice of which problems could be solved in StepWise mode versus requiring full scaffolding.
This research revealed a key insight: learning tools must respect how students naturally think—messy, iterative, and nonlinear. The most successful features were those that met students where they were, not where we wished they would be.
Student interviews and instructor workshops shaping the platform design
Design Philosophy: Errors as Learning Opportunities
A core principle that guided every design decision was treating errors not as failures to be penalized, but as learning opportunities to be explored. This philosophical shift from traditional grading systems shaped the entire platform.
How this manifested in the design:
- Inline feedback bubbles: Rather than marking answers wrong and moving on, the system provides guidance to help students understand and correct their misconceptions
- Multiple attempts without penalty: Students can revise their work after receiving feedback, learning from mistakes without grade anxiety
- Progress over perfection: The platform celebrates growth and improvement, not just final correctness
- Scaffolding that fades: As students demonstrate competence, the system gradually reduces support, building independence and confidence
This approach balanced pedagogical rigor with interface simplicity. The platform needed to be mathematically precise while remaining approachable and forgiving, respecting that learning is inherently messy and non-linear.
Impact and Adoption
Aktiv Mathematics was adopted across hundreds of universities and K-12 bridge programs, helping students build foundational math skills from Prealgebra through Precalculus.
Measurable outcomes included:
- Improved student engagement: Students spent more time working through problems and showed reduced frustration compared to traditional homework systems
- Enhanced instructor visibility: Professors gained unprecedented insight into student problem-solving processes, allowing for more targeted interventions
- Reduced cognitive overload: The scaffolded approach helped students build confidence without feeling overwhelmed by complex problems
- Better learning outcomes: Students demonstrated improved understanding of foundational concepts and higher retention rates
The platform received U.S. Patent #12,198,567 B2, recognizing the innovative approach to step-by-step mathematical instruction and feedback systems.
In 2024, Aktiv Learning was acquired by Top Hat, bringing the platform to an even larger audience of students and educators as part of Top Hat's comprehensive education technology ecosystem.
Key Takeaways
Working on Aktiv Mathematics taught me profound lessons about designing educational technology that actually helps students learn:
- Respect how students think: Learning is messy, iterative, and nonlinear. Tools that try to force students into rigid workflows fail. The best designs meet students where they are.
- Context matters more than correctness: Simply marking answers right or wrong teaches nothing. Students need to understand why their approach worked or didn't work.
- Errors are data, not failures: Mistakes reveal misconceptions. Treating errors as learning opportunities rather than penalties fundamentally changes the student experience.
- Visibility enables teaching: Instructors can't help students if they only see final answers. Showing the reasoning process transforms homework from assessment into a teaching tool.
- Scaffolding should fade: The goal isn't permanent support, but building independence. Systems should adapt support levels based on demonstrated competence.
- Domain expertise is essential: Deep understanding of mathematics pedagogy and how students develop mathematical thinking was critical to making effective design decisions.
